Curvature-Guided Solve Process
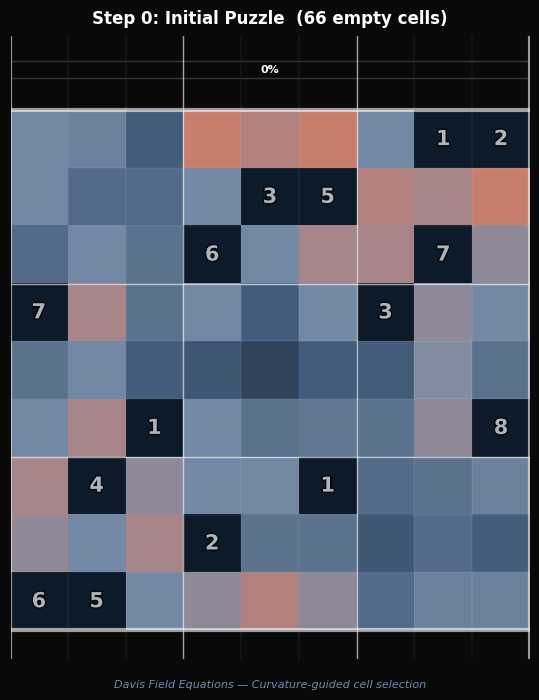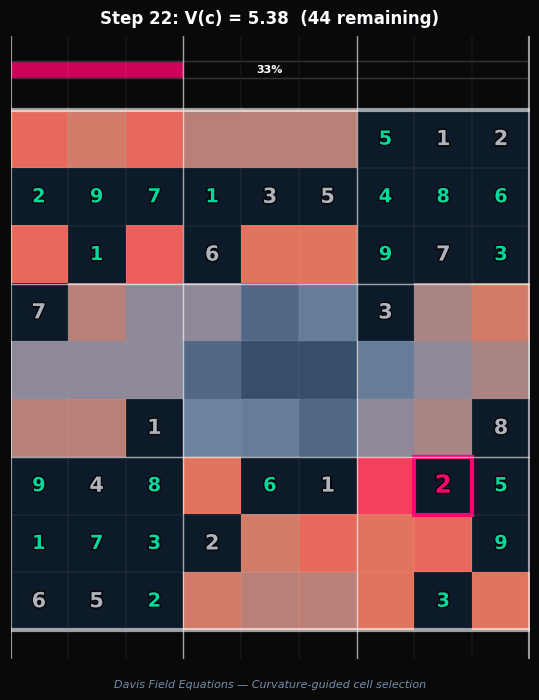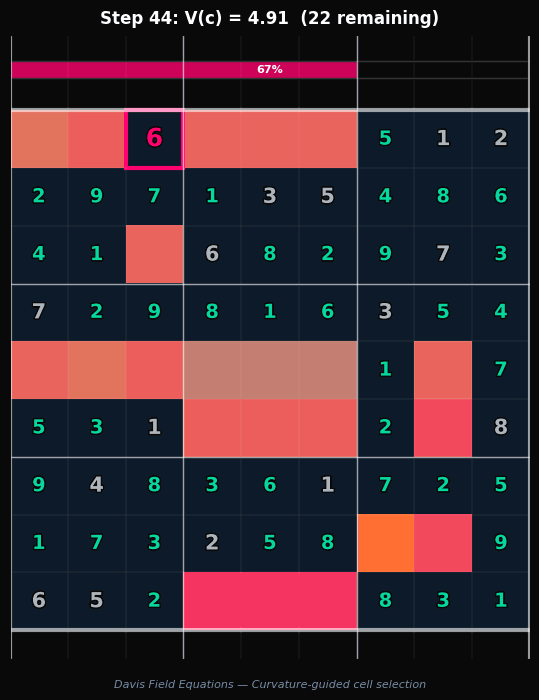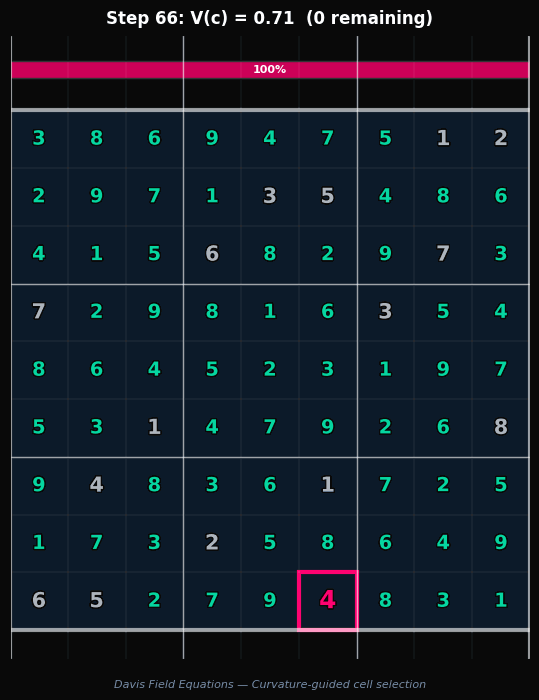
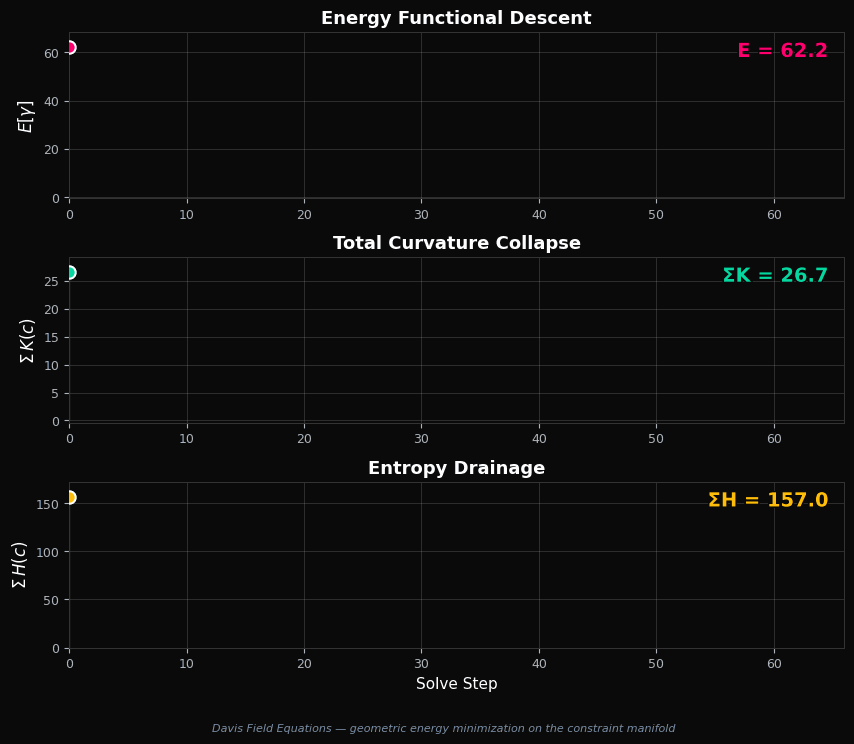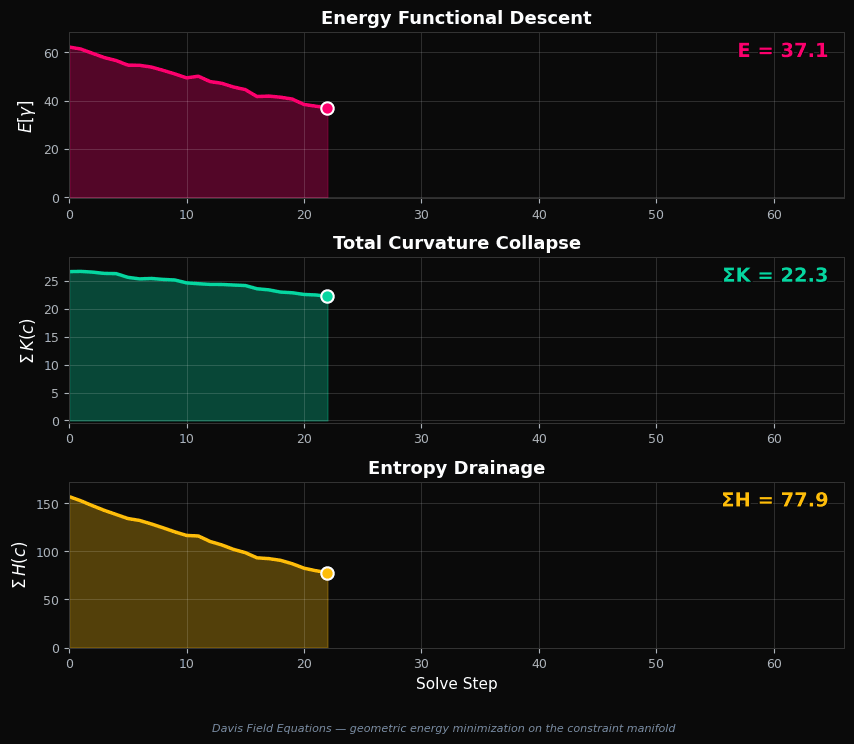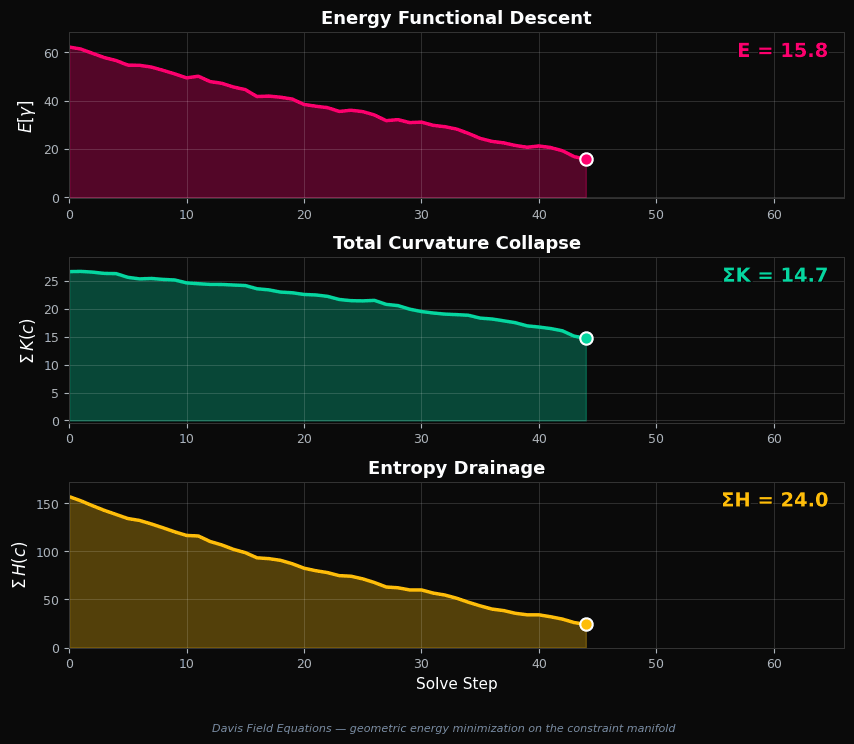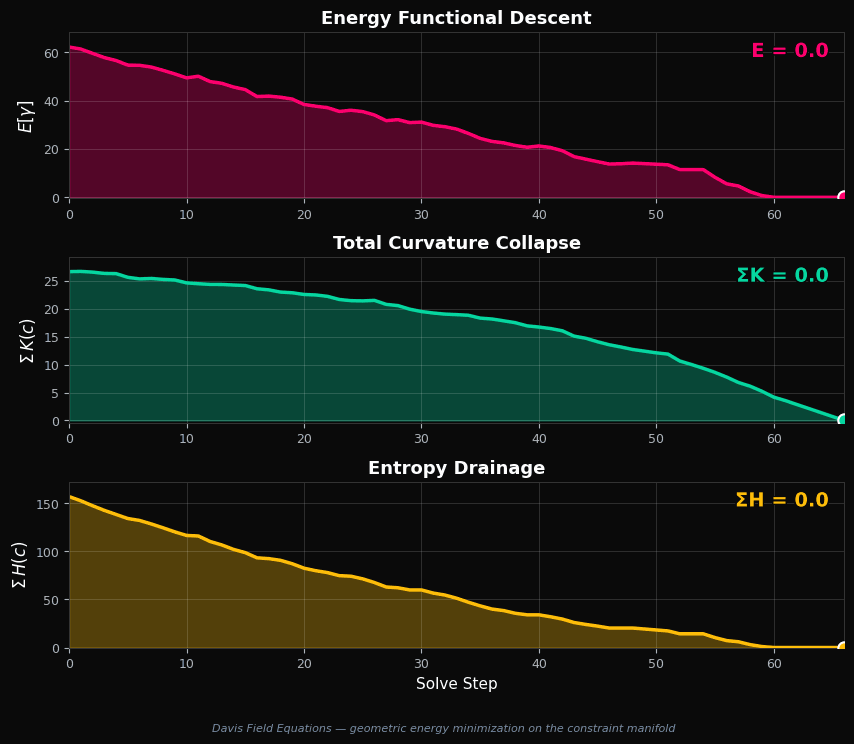
Watch the solver trace a geodesic through the constraint manifold. At each step, the cell with the highest information value $V(c)$ is resolved first, and the curvature field collapses monotonically toward zero.
GPU-accelerated constraint satisfaction guided by intrinsic Riemannian curvature. A geometry-aware solver that crushes the world's hardest Sudoku at 1,226× speedup over Python CPU — and generalizes to any finite-domain CSP.
40,128× faster than Kona 1.0 Yann LeCun’s EBM solves one puzzle in 313ms. We solve 270,000 per second.Computational resources should flow toward regions of highest curvature — where they have the greatest marginal impact on constraint resolution. Classical GPU approaches treat every vertex equally. The Davis manifold tells you where the hard work is, before the work begins.
The solver implements a three-phase CUDA pipeline derived from the Davis Field Equations. A trichotomy parameter Γ automatically classifies each instance by its geometric complexity and routes it to the optimal phase combination — no manual algorithm selection required.
Classical heuristics — MRV, degree heuristic, checkerboarding — all emerge as degenerate cases of the curvature-guided ordering when specific curvature weight components are set to zero. The Davis manifold framework subsumes and unifies them.
The constraint graph induces a discrete Riemannian manifold in the sense of Regge calculus — not a metaphor, but a genuine geometric structure with a metric tensor, connection, and holonomy group. The local curvature field measures three independent scalar invariants of the constraint fiber bundle.
The trichotomy parameter $\Gamma = \dfrac{m \cdot \tau}{\hat{K}_{\max} \cdot \log |S|}$ classifies instances by the ratio of assigned structure to geometric complexity, automatically gating them into the optimal phase combination.
Watch the solver trace a geodesic through the constraint manifold. At each step, the cell with the highest information value $V(c)$ is resolved first, and the curvature field collapses monotonically toward zero.


Evaluated on 15-clue extreme Sudoku (66 empty cells, Γ ≈ 0.19) — the hardest class of well-posed puzzles. All 11 hardest-known instances solved in under 9ms on a consumer laptop GPU (NVIDIA RTX 5070, Blackwell architecture). Solver v4 averages 7.8ms per puzzle.
The framework is not a Sudoku solver. It is a general-purpose GPU execution strategy for any finite-domain constraint satisfaction problem. Any CSP expressible as variables with finite domains and pairwise constraints admits a Davis manifold whose curvature field guides GPU scheduling.
The GPU architecture targeted in this work bears the name of David H. Blackwell (1919–2010), the first Black scholar inducted into the National Academy of Sciences and a pioneer of dynamic programming, Bayesian statistics, and game theory. The sequential decision-making under uncertainty at the heart of constraint satisfaction is precisely the domain Blackwell formalized.